Statistics
In this lecture we will see how we can approximate parameters to mathematical models using data.
Introduction
We often want to build models to understand how systems in the real world function. For example, imagine a company has a manufacturing process. We might want to understand how efficient this is. Very often we need to do this without being able to 'look inside' the system we are measuring. For example, we do not need to accurately model each stage of a manufacturing process to be able to assess it's overall efficiency, or to compare it against other processes that might be more or less efficient. Instead, we can collect statistical data about the process as a whole, treating it as a 'black box'.
For another example, imagine a music recommendation system. Such a system tries to model the preferences of a particular user by collecting statistical data about the user's behaviour. We cannot actually open up a user's brain and look inside.
Whatever we are modelling, we can observe the system as a whole and collect measurements or data. These measurements are likely to involve error or uncertainty. We use this data to create a statistical model of the system. From this statistical model we can generate insights such as:
- How does the system behave?
- What is a typical value?
- Are the patterns in the data meaningful or due to chance?
To do this, we need to understand the underlying probability distributions that generate our data. Based on assumptions about these, we can assign probabilities to different observations and make judgements about how likely or unlikely certain observations are.
Learning Outcomes
- Recognise common probability distributions
- Identify the type of data of a range of variables
- Identify dependent and independent variables
- Appropriately use measures of central tendency to describe data
- Calculate Arithmetic Mean
- Calculate Median
- Calculate Mode
- Appropriately use measures of spread to describe data
- Calculate Range
- Calculate Inter-quartile Range
- Calculate Variance
- Calculate Standard Deviation
- Calculate measures of correlation for paired data
- Approximate the parameters to a normal distribution from data
- Perform a linear regression to model a linear relationship between variables
Overview
Probability Distributions
A probability distribution defines the values that a random variable can take, and the likelihood of it taking those values. We will see how probability distributions are defined.
Different real-world systems obey different probability distributions. The most common probability distribution in nature is the normal distribution. However, a great many probability distributions have been studied. There is an enormous list on Wikipedia
Random Variables
A variable represents a value we are uncertain of, such as:
- The result of rolling a dice
- A experimental participant's reaction time
A random variable is a variable that can take different values. it is a mathematical way of abstracting the result of an experiment. The probability of this variable taking any particular value is defined by a probability distribution.
We usually write variables using capital letters, e.g. \( X \). The probability that a variable $X$ takes the value \( x \) is written
Dice Example
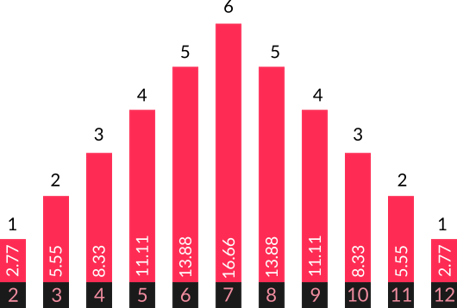
When you roll a dice, you are equally likely to get each number. When you roll multiple dice and add them together, the likelihood of each value differs. These two experiments have different probability distributions. Many board games and tabletop games exploit the different probability distributions you can create by adding together dice of different types.
Discrete Uniform Probability Distribution
Imagine we are rolling a fair dice. We can model the dice as a random variable, \( D \). What is the probability distribution that defines this variable? (i.e. with what likelihood does it take different values?)
Discrete probability distributions have values that are
- disjoint
- collectively exhaustive
In this situation, the values that \( D \) can take are discrete. You cannot be half-way (or four seventeenths of the way) between two numbers on the dice. The possible outcomes for a discrete random variable can be counted. In this case, listing them is easy (this is also the sample space of our experiment):
A probability distribution is defined by a function. For a discrete distribution, the particular type of function is called a probability mass function .A probability mass function maps outcomes to the probability of that outcome.
The probability of getting a particular value \( x \) on the dice is defined by the function:
Using the interactive dice roller on the slide for this section, observe how the frequency of each value when rolling a dice slowly converges on this value.
If we sum a probability mass function for all possible values \( x \) (here values on the dice, but in general any outcome in its sample space \( S \)), we get 1. In other words, it's always going to take one of the possible values - it cannot not take a value.
Binomial Distribution
Instead of rolling a dice, imagine flipping a coin \( n \) times and counting the number of heads \( x \). If you repeat this experiment enough times, you will see that the number of successes will be distributed according to a binomial distribution. The probability mass function for a binomial distribution is:
This applies to any experiment where you are repeating a task with a constant probability of success \( p \) and counting the successes.
Play with the interactive coin flipping example on the slides. Observe how the probability distribution takes on a distinctive shape. This is the shape of the binomial distribution.
Picking from a continuous distribution
We have seen two examples of discrete distributions: rolling a dice and flipping a coin. In these cases there are a finite, discrete number set of possible outcomes. However, the response time of a webserver, for example, is continuous. It could be any of an infinite number of values.
Continuous distributions are defined by a continuous curve called a probability density function. This curve gives the relative likelihood of a value being selected. However, the likelihood that any particular value will be selected from a continuous distribution is 0. This is because there are an infinite number of values that could be picked. However, we can calculate the probability of picking a value within a given range by using calculus to calculate the area under the curve for a given range. The area under the whole curve equals 1.
Continuous Uniform Distribution
Consider a uniform probability distribution, between and . The probability density is the same for all values. The probability density function is:
\[ f(x) = \frac{1}{ 10 - 0 = 0.1 \]You will see that the plot shows a probability density of \( 0.1 \) for all values. However, this does not mean the probability of drawing any particular value - say 5 is \( 0.1 \). The probability density at a particular value is not the same as the probability of generating $x$. With a continuous probability distribution, the likelihood of a particular value being chosen is always 0. Consider: in a continuous distribution there are an infinite number of values the variable could take. The likelihood of picking a particular value is thus \( \frac{1}{\infty} = 0 \)
We can, however, reason about the probability of drawing a value in a particular range. This is because the probability is given by the area under the probability density function.
To find the area under a function we need to use calculus; specifically integration, which is beyond the scope of this course. However, briefly, the integral of a function $f(x)$ gives a function that is the cumulative area under $f(x)$ (i.e. the area so far).
\[ \int \frac{1}{ 10- 0} dx = \frac{x}{10-0} \]We can solve this within limits by substituting upper and lower values for $x$. The likelihood of picking a value of our continuous uniform variable $Y$ between
Lower limit: Upper limit: is:
\[ P( 10 < Y < 0) = \int_{10}^{0} f(x) dx \]\[ = (\frac{ 0}{ 10-0}) - (\frac{10}{10-0}) \]\[ = -1 \]Normal Distribution
Many real-world variables have a characteristic distribution.
Normal distributions are the most common probability distributions found in nature. This is because where a variable is the combination of a large number of variables it will converge on a normal distribution, according to the Central Limit Theorem.
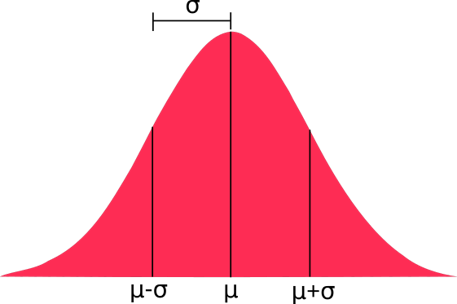
Normal distributions (also called Gaussian distributions) are defined by a complicated-looking function that takes two parameters: mean ( \( \mu \)) and standard deviation (\( \sigma \)).
The probability density has the shape of a bell curve. Values close to the mean are likely, while values far from the mean are unlikely. How stretched this bell curve is is controlled by the standard deviation.
In the following graph, notice how the shape of the distribution does not change with different values for mean ( \( \mu \)) and standard deviation (\( \sigma \)). Only the scales of the axes change:
As before, if we wanted to find the probability of drawing a value in a particular range we would need to integrate this function. The probability of drawing a particular value from the normal distribution is 0.
Finally, if we find the total area under a probability density function i.e. integrate between the limits of the lowest and highest values a variable can take, it would be 1. In other words, the probability that you are going to get some value within the distribution is always 1.
Data Collection
Samples and Populations
Variables
In an experiment we may control one or more variables. These are called dependent variables. In a simple experimental study design we would manipulate one variable and then observe the effect on a second variable.
For example, say we want to observe the effect of caffeine consumption on sleep. We might control how much caffeine a number of people consume (dependent variable) and then measure their quality of sleep (independent variable).
Types of Data
Variables can be of different types.
Nominal
Question: What is your favourite animal?
In nominal data, each data point is a 'name' or label. For instance, someone's favourite type of animal. Such data cannot be put into a meaningful order. We cannot do much more with nominal data than count the frequency of each category and use this to approximate the underlying probability mass function. The probability distribution underlying a nominal variable will be discrete. For example, the variable \( X \in \{cat, dog\} \) might be defined by the probability mass function:
By observing many instances of $X$ as either cat or dog we will be able to approximate these values.
Ordinal
Question: How much time do you spend thinking about mathematics?
Each data point is a value in an ordered list. The order of values in this list is meaningful, but the ratio between them is not. For example, asking someone to choose between 'strongly agree', 'agree', 'disagree', and 'strongly disagree'. 'Agree' is certainly more positive than 'disagree', but not necessarily by the same difference as between 'disagree' and 'strongly disagree'.
Being discrete, ordinal variables will also be defined by probability mass functions. However, in practice we can often assign numbers to each category and then treat them as if they were numeric.
Numeric / Ratio
Question: How high is the ceiling in your room in meters?
Each data point is a numerical value, i.e. a number. The ratio between such values is meaningful. If someone is 6 feet tall, we know they are exactly twice the height of a 3 foot tall child.
Numeric variables are drawn from continuous distributions, commonly (but certainly not always) the normal distribution. By collecting enough data we can approximate the distribution that generated the data. Often we are more interested in asking whether data are normally distributed, whether they are drawn from a particular normal distribution, or whether two sets of observations are drawn from the same distribution.
Measures of Central Tendency
Measures of central tendency are statistics that have been invented to locate the 'middle' of a set of data. They provides a typical or representative value, for questions such as:
- Does this cost more or less than average?
- How quickly am I downloading data?
Arithmetic Mean
The most common meaning of 'average' and widely used as a summary statistic to describe a dataset. The arithmetic mean is equal to the sum of the values, divided by the number of values: \( \overline{X} = \frac{1}{n}\sum X \). This calculation is only suitable for numeric data. It is sensitive to extreme values (outliers) due to its method of calculation. The mean is one of the parameters to the normal distribution. As such, it is used by some statistical tests, such as the $t$ test to compare whether one data set has significantly larger values than another.
Median and Quartiles
To find the median, put the values in order and find the one in the middle. If the data set has an odd number of values, there will be a middle value. If the data set has an even number of values, the middle will be between two values. If the middle is between two values, one finds the mean of these two (if possible).
The median is suitable for ordinal and numeric data, but not for nominal data. The median is often used as a statistic for comparing non-parametric data (i.e. data that doesn't follow a normal distribution). The median is robust in the presence of outliers, because a single value is unlikely to significantly affect the median.
Quartiles are values that divide the data into four approximately equal parts. These are found by first ordering the values smallest to largest.
The second quartile ($Q_2$) is the same as the median. It is the value in the middle of the data set. 50% of the data is above and 50% of the data is below this point. If we take only the values *below* the median ($Q_2$) and find the median of this set, we get the first quartile ($Q_1$). If we take only the values *above* the median and find the median of this set, we get the third quartile ($Q_3$). The first and third quartiles are positioned at 25% and 75% of the way through the data respectively.
Mode
The value that occurs the most times in the data set, found by counting the occupancies of each value. This is suitable for all types of data and is the only measure of central tendency suitable for nominal data.
Measures of Spread
Measures of spread are statistics that describe how bunched together or spread out a set of data are. Do all our measurements report similar values, or is there a wide variation in values?
Range
Range is the crudest and easiest measure of spread to calculate
The range is the difference between the highest and lowest value. It is extremely sensitive to outliers, as outliers, if they exist, will be the minimum or maximum value and thus used for this calculation.
Inter-quartile Range
The range of the middle 50% of the data. This is the difference between the upper and lower quartiles. The IQR is more resilient to outliers than the range, as the most an outlier will do is shift the quartiles only slightly.
Variance
The square of the average difference between a value and the mean. There are two ways of calculating variance. $\sigma^2$ is used to give the variance of a population. If we are calculating the variance of a sample we get a better approximation by dividing by $n-1$ instead of $n$. We notate the variance of a sample as $s^2$.
Here and elsewhere an overline is used to indicate the arithmetic mean of a variable. Thus \( \overline{x} \) is the mean of the variable $x$.
Standard Deviation
Standard deviation is the square root of the variance. It similar differs between population $\\sigma$ and sample $s$ variants.
To select the correct formula you must device whether this data represents the entire population, or whether you approximating the standard deviation of a wider population from data that represents only a sample of that population.
Outliers
When measuring a variable we sometimes observe extreme values that do not fit the general pattern of the data. This might be caused by an error in measuring or because the individual that we are measuring is particularly unusual.
For example, imagine we measure basketball proficiency by counting the number of times a person can throw a ball through a basketball hoop and one person gets a score far higher than anyone else. It might be that we miscounted or made a transcription error when entering the data (i.e. the value recorded is not the correct value). Alternatively, it might be that they are a professional basketball player. If we were expecting to study the general population, including the score of a professional basketball player might bias our statistics.
It often isn't possible to know for sure whether a value should be included. We often cannot tell after the fact whether a measurement error was made, for example. By identifying outliers solely from the data we risk systematically excluding legitimate data points just because they do not fit our expectations. This can make the data look appear to be drawn from a distribution that is less spread out than it really is.
There are various methods that exist to identify outliers. One such method is Tukey's Fences. Let $k$ be a constant. A typical value for $k = 1.5$. A measurement is an outlier if it is outside the range
Where $Q_1$ and $Q_3$ are the first and third quartiles.
Correlation
When we have pairs of observations for two variables, we can ask whether there is any observable relationship between them. For instance, we might measure height and basketball ability or compare the sizes of people's feet with the sizes of their best fitting shoes.
We can plot these using a scatter plot. Each data point consisting of a measurement of each of our two variables is plotted on x- and y-axes.
There seems to be a relationship between these two variables. As foot length increases, shoe length also increases. This relationship appears to be linear: as foot length increases, shoe length increases at a rate that is approximately a constant proportion of foot length. When there is a linear relationship between variables, we can draw a line of best fit through the data, as below. This is a straight which minimises the overall distance between each data point and the line.
Calculating Correlation
The degree to which the data follows such a linear relationship is called its correlation. The better the data follows a straight line, the stronger the correlation.
One method of calculating a correlation is Pearson's r, or Pearson's product-moment correlation coefficient. The data is paired, so $x_i$ and $y_i$ refer to the $x$ and $y$ value of the $i$th data point. \( \overline{x} \) and \( \overline{y} \) are the means of the $x$and $y$ values. This formula can also be written in several different ways.
Spearman's Rho
Pearson's $r$ assumes data is parametric. Spearman's $\rho$ (rho) is a measure of correlation for non-parametric data
Checks for monotonic relationship between variables
Works by calculating Pearson's r on ranks (i.e. you only care about order, not exact values).
Linear Regression
Now we have observed that the relationship between shoe length and foot length approximates a straight line, we might want to model this straight line as an equation. If $y$ is shoe length, and $x$ is foot length, we want to find values $a$ and $b$ such that the formula below approximates the straight line relationship:
If we had such an equation, then we could convert any foot length into the appropriate shoe length, even when we had not measured someone with exactly those size feet. To do this, we can use a linear regression.
Linear Regression
A linear regression models a linear the relationship between independent and dependant variables
A linear regression works by modelling each point as $y_i = a + bx_i + \epsilon_i$. We can understand the term $\epsilon_i$ as the amount of error between our $i$th point and our straight line defined by $y=a + bx$. We then want to find values of $a$ and $b$ such that the sum of $\epsilon$ is as small as possible. In other words, we want to minimise the overall error.
Least Squares Method
One approach to finding $a$ and $b$ is the least squares method. We can plug out values into the following formulas for the values of $a$ and $b$ in terms of the values of $x$ and $y$.