Models of Computation
In this lecture we are going to learn about models of computation and computability.
We are following the goal of building a model of a computer.
Learning Outcomes
- Describe the mapping account of computation
- Give three examples of models of computation
- Interpret a FSM diagram
- Interpret and use Kleene star notation for describing regular languages
- Determine whether a finite state machine accepts or rejects a string
- Describe the language that is accepted by a simple provided FSM
- Reason whether given simple problems can be decided by any finite state machine
- Check whether a transition is permitted within a given Rewriting System
- Generate derivations in a rewriting system and provide terminal words
- Generate and reason about the language generated by a rewriting system
Introduction
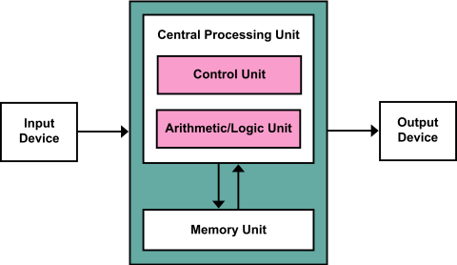
We usually think of computers as
- Magical boxes with user-friendly interfaces
- von Neumann architecture
But that's just what we're used to. For most of history, "computers" were human. Calculations were broken down into steps and then performed by teams of people.
We can also imagine computation being performed by other physical systems. Slime mould computes the shortest path, e.g. through a maze or a topographical map of the US. The conductive properties of a lump of carbon nanotubes when perturbed by small currents can be used to perform computation. Inputs are encoded into voltages and the output voltages is the 'result' of the computation.
(Adamatzky, 2013)
(Dale et al., 2017)
The Mapping account of computation
A physical system performs computation when there is a mapping between states of the system and computational state
Let's remove the physical world from this picture. What's left?
- States in a model
- Rules of transition
We will call this a formal system model
Computers perform computation by physically instantiating problems
We can also understand computation mathematically as a formal system
The Mapping account of computation
Overview
In this lecture we will see three models of computation.
The first model of computation we will look at is the Finite State Machine. We will see how finite state machines can be used to model certain kinds of computation. We will see how we can create finite state machines to perform computation such as accepting or rejecting input strings. We will also look at some of the limitations of finite state machines.
Next we will briefly look at Turing Machines and see some inherent limitations in the power of computation.
Finally we will look at string rewriting systems. Rewriting systems are formal systems, and understanding the mechanics of string rewriting will help us to understand formal logic over the next several lectures.
Finite State Machines
A finite state machine is a simple and useful model of computation, though one that has limitations on the computational problems that it can solve.
An abstract machine is a description of a computational system that can precisely defined in mathematics. There are various types of commonly discussed abstract machine. We will look at two in this lecture: Finite State Machines, and Turing Machines.
Turnstile Example
Finite State Machines let us model certain kinds of computational system. For example, imagine a coin-operated turnstile, like you see at the entrance to toilets in the London Underground. The turnstile starts as locked. If you enter a coin, it unlocks, allowing you to push through the turnstile. Once you've pushed through, it locks after you to require the next person to enter a coin before they can enter. This is represented in the following state diagram:
A finite state machine can be in one of a set of states. For example, 'locked' and 'unlocked' in the above example. When it receives an input symbol it transitions to a new state according to a set of rules. These rules describe:
- The state the machine must be in for the rule to apply
- The input symbol that triggers the rule
- The new state the machine transitions to (this may be the same as its current state)
- When the turnstile is in the 'locked' state
- and it receives the 'coin' symbol
- transition to the 'unlocked' state
Turnstile example
CC BY-SA N/A 4.0 (Via Wikipedia)
Formalising an FSM
The basic components of a Finite State Machine are:
\( \Sigma \) - Input alphabet. This is a set of symbols that the FSM can receive as an input
\( S \) - Set of states the FSM can be in. This set is finite (hence the name Finite State Machine).
\( s_0 \) - Initial state; the state the machine begins in before it reads the first symbol.
\( \delta : S \times \Sigma \rightarrow S \) - Transition function; the rules that tell the machine what to do when it is in a given state and receives a given input symbol.
Input tape
We often think about what happens when an FSM receives a given sequence of input symbols. We will call the string of input symbols that the machine receives as the input tape. This term comes from the design of the Turing Machine (which we will see later on) which is described in terms of physical tapes.
For example, if the turnstile received the following inputs, what state would it be in?
| Coin | Push | Coin | Push | Push | Coin |
We can work through a description of the turnstile FSM to find out that the machine would be in the 'Unlocked' state. Indeed, here is an interactive Finite State Machine tool. You can step through the computation below to see how each rule applies as the FSM works through the input tape.
| Finite State Automaton Rules | |||
|---|---|---|---|
| Starting state | Input tape: | ||
| State | Input | Go to | |
| Finite State Automaton | |||||||
|---|---|---|---|---|---|---|---|
| Read head | |||||||
| Input tape | C | P | C | P | P | C | |
| Current state | Locked | ||||||
Classify strings using an FSM
What would happen if we had no rule in our turnstile FSM to handle what happened if you were in the 'Unlocked' state and a coin was entered? We would not know what state to transition to, and the computation would crash. Thus we can design FSMs that crash on certain inputs.
We can then ask the question: what input tapes does a given machine crash on? Equivalently, what tapes does a given machine accept?
Let's take out two of the rules from our turnstile FSM. Now there is no rule to describe what happens if we are in the 'locked' state and receive the 'Push' input, or what happens if we are in the 'unlocked' state and receive the 'coin' input.
Now we see that the string we considered above CPCPPC causes the FSM to crash. We will say this string is rejected by the FSM.
| Finite State Automaton Rules | |||
|---|---|---|---|
| Starting state | Input tape: | ||
| State | Input | Go to | |
| Finite State Automaton | |||||||
|---|---|---|---|---|---|---|---|
| Read head | |||||||
| Input tape | C | P | C | P | P | C | |
| Current state | Locked | ||||||
Languages
What strings are accepted and what strings are rejected by this FSM? We will call the set of accepted strings the language accepted by this FSM.
| Accept | Reject |
|---|---|
| CP | P |
| CPC | CPP |
| CPCP | CCP |
| ... | ... |
Different kinds of abstract machines can recognise different kinds of language.
Limitations of Finite State Machines
We can reason about any computation in terms of the accepting or rejecting of given strings (though this is not the only way or always the most useful). That is, we can describe the computational power of an abstract model of computation in terms of the kinds of languages that it can accept.
Let's take the example of detecting palindromes. A palindrome is a string that is the same forwards as backwards. For example, the word 'racecar' is a palindrome.
Turing Machines
| Turing Machine Rules | |||||
|---|---|---|---|---|---|
| Starting state | Input tape: | ||||
| State | Input | Write | Go to | Move | |
| Turing Machine | |||||||
|---|---|---|---|---|---|---|---|
| Read head | |||||||
| Tape | 0 | 1 | 0 | 0 | 1 | 0 | |
| Current state | Start | ||||||
| Time taken | 0 | ||||||
Physical Turing machine model
CC BY 3.0 Rocky Acosta
Rewriting Systems
Over the next several weeks we are going to build directly on the idea of formal systems to model human reasoning using logic. However, all of mathematics might be understood as a kind of formal system.
When we are talking about something being 'formal' we mean something that obeys strict rules. If we make a formal model of a system, then we can only manipulate that model according to its rules. Take algebra for example. We are not allowed to rearrange the equations shown above however we like. For our answer to be valid we have to always follow the rules of algebra.
One type of formal system is a rewriting system.
A rewriting system is a set of rules that transforms strings into other strings
Alphabets and Words
If $Σ$ is a finite alphabet of symbols, then let $Σ^*$ be the set of all finite length strings that can be formed using symbols from $Σ$
So given the alphabet \( Σ = \{a, b\} \) we have the set of words on $Σ$:
$ \epsilon $ represents an empty string.
Each state in our rewriting system is a word on $Σ$, meaning it is a string formed of symbols in our alphabet
For example, we might have the words:
Rewriting Rules
The rules of a rewriting system allow us to transform one string into another by substitution. The following rule allows us to replace one instance of the symbol $a$ with $b$
We call such rules that operate on symbols in $\Sigma$, $\Sigma$ rewriting rules. A $Σ$ writing system is a finite list of such $Σ$ rewriting rules \( \alpha_1 ↷ \beta_1, \dots, \alpha_n ↷ \beta_n \)
Transitions in a rewriting system
In a rewriting system, rewriting rules apply to only a single substring at a time. Thus if we had the rule $a \curvearrowright b$, and we had some word $\dots a\dots$, we could derive a new word by replacing that $a$ with $b$, and leaving the rest of the string untouched: $\dots b\dots$
If we can obtain a word by a single application of a rule in $P$, we will write this as:
Which we will read "$B$ can be obtained from $A$ in one step under rules $P$"
A derivation in rewriting system $P$ is a list of words $A_1, A_2, \\dots, A_n$ so that
We allow derivations of length zero. So we will always have $A ⇒^* A$
Derivation Question
Given the rewriting system
Is it possible to derive $aabb$ from $X$?
Yes, here is an example derivation:
Languages
Grammars
Definition: A grammar is a rewriting system $P$ together with an initial word $I$. Such a grammar $(P, I)$ generates the language
A word $W$ is terminal in rewriting system $P$ if there is no other words that can be derived from that word.
A language is a set of all possible terminal words generated from a grammar. That is, given initial word $I$ in $\Sigma^*$ and set of $\Sigma$ rewriting rules, the language $L$ is defined as the set of all words derivable from $I$ from which no further derivation is possible.
For example, the initial word $X$ and rules
Generates the language \( \{ab, aabb, aaabbb, aaaabbbb, ... \} \). Note that the symbol $X$ never appears in this language as due to the rules above $X$ can never be in a terminal word. Thus while words such as $aXb$ and $aaXbb$ can be derived from this initial word, it is not included in the language this grammar defines.
Example Language
Consider the alphabet \( Σ = \{ a, b \} \) and the $\Sigma$ rewriting system \( P = \{ ab ↷ a \} \). Lets say we have the initial word \( I = abbb \). Note that $I ∈ Σ^*$.
We can consider the language or the subset of $\Sigma^*$ defined by this grammar. In this case, the language contains exactly one string: $a$. Here $a$ is the only terminal word in the grammar.
What is the language?
You have the grammar
What is the language generated by this grammar?
We attempt all possible derivations and find the unique terminal words:
The language generated by this grammar is
Summary
Turing Machines
Universal model of computation
Rewrite symbols on tape
Move left or right
Decision Problem
Any problem can be represented as a decision problem
Some problems are uncomputable (e.g. Halting Problem)